Fish Locomotion:

Bio-mimetics is a field of mimicking how form matches function in natural systems. As such before analyzing how the form of a fish ray effects its function we must first have an understanding of what its function is. Fish swim using a combination of three different propulsive techniques: Undulation, Rowing, and Lift.

Undulation:

Undulation is the process of fish propulsion through wavelike motions of a portion of a fish’s body. These wavelike movements push backward on the water thus propelling the fish forwards. To optimize forward motion thrust must be maximized while drag and any lateral forces minimized. The amplitude of undulations along with surface area of the interacting part typically increases from head to tail along the fish’s body. This results in greater force generation.

Examples of Undulating Fish: Tuna, Shark, and Eels

Rowing:

Whereas propulsion by undulation is obtained by the movements of the fish body and more specifically the caudal tail, propulsion by rowing is obtained through the motions of the pectoral and pelvic fins which are also known as paired fins (Sfakiotakis). This method is broken up into two main motions: the power stroke and the recovery stroke. The power stroke is the first half of the motion where the paired fins move backward with respect to the body. When the fins flip backward they push on the water behind them. During the motion of the fin, drag is induced opposite to the direction of the fin. During the power stroke this drag points in the forward direction (from fish tail to head) while in the recovery the drag is opposite. These drag forces act to push the fish in the direction they act. It follows that in order to maximize forward efficiency of rowing drag should be zero during the recovery stroke and greatest during the power stroke. The shape and flexibility of the fish’s fins have a large impact on the drag coefficient and as a result directly relate to the efficiency of motion.

Lift-Based:

In lift-based propulsion however animals do not need to push backward on the water. Animals that swim using this method use their fins as wings. Lift is created when there is a pressure difference between the top and bottom of the wing. In order to keep the lift with a component facing forward animals adjust the angle of attack by rotating and swinging their "wings". It is however important to note that the lift forces in addition to providing forward movement will also provide up and down motion. To balance these vertical forces the animal must alternate positive and negative angles of attack. This process causes an oscillatory motion of the body and somewhat decreases the efficiency.

Fin Structure:

Many fish possess ray-reinforced caudal, dorsal, pectoral, or ventral fins. These fish fins are best described as an anisotropic bio-membrane. Ray-reinforced fins are composed of parallel fin rays embedded into a collagenous membrane. The rays act as the skeleton of the fin providing most of the structural stiffness while the membrane provides the desired shape and shear stiffness. As it is the outer surface of the fin, the membrane’s structural properties play a crucial role in the fins hydro-dynamic performance. The fish membrane is formed from a material called collagen, a naturally occurring protein. Collagen is a very strong structural protein which typically forms into triple helix 'ropes' as seen below. These fibers, as do any cable, exhibit low bending stiffness (0.3 to 1 MPa) but high axial tensile strength. When a network of collagen fibers link together in a mesh they create a sheet (or membrane) with a resulting high in-plane tensile strength. While this membrane helps to provide the surface area of the fin the embedded rays work as it's structural backbone.

The ray structures serve to transfer forces exerted on the membrane from the surrounding water to the body of the fish and vice versa. Due to their form the embedded rays exhibit high bending stiffness and flexibility with a modulus of about 1 GPa. According to morphological studies, fin rays have a bi-laminar structure with two small segmented bony elements called hemitrichs. These two segments surround a central bundle of collagen which sits in the gap between them. These elements are paired and resemble a bimetallic strip with two elongated bony elements separated by a central collagen core. There are short ligaments and elastic fibers located along the length of a hemitrich and at the ends. Rays are connected at their base to the cartilage and skeletal system of the fish. At this junction there is a system of muscles which provides multi-degree of freedom movement of the rays.

Structure of a Collagen Fiber	Overview of Rays in a Fin

Fish fin rays are unique from bones and cartilage in their controlled flexibility. Flexibility is obtained through muscular manipulation of the bi-laminar structure of the ray. Each ray is attached at its basal end to four separate muscles. Two muscles attach to each of the bi-laminar rods (hemitrichs). This set up allows the fish to control each hemitrich separately. By activating the muscles on one side of the hemitrichs while leaving the other inactive the fish can induce a curvature in its fin. The ability for the fish to control their fin shape in this fashion is called active control. It follows that the bi-laminar structure allows fish to actively alter the propulsive surface by choosing which muscles to activate at any given time. A fish's ability to control the curvature of its fins allows it to not only control the rate of flapping but also the deformation at any specific point in time. The theory is that this ability for active control would increase efficiency of the fin-flapping propulsion mechanism.

Modeling:

Due to the intricacy of fish fins structure any analysis model has to be very detailed. As a result developing an accurate model was an iterative process. Initially we developed a 9-ray caudal fin model to analyze the effects the flexible rays have on propulsion efficiency in a sway motion. Building off of this model we developed a 15-ray pectoral fin model to study the effect of the flexible rays on lift-based swimming. Then based off of the previous two models a more complicated 12-ray model was developed. This model was intended to study the effect flexible rays have on a labriform swimming technique with a combination of rowing and lift-based techniques. Although multiple different tests were run the basic numerical simulation of each was the same.

In each of the models an immersed boundary model based on the Navier-Stokes equations was used to model the fluid interactions. In analyzing the structural components of the fin the rays were modeled under the Euler-Bernouli method and the membrane was modeled as a system of linear springs.

Since the rays functioned as a skeletal support to the otherwise flimsy fin membrane they were modeled as beams much the same as in the analysis of any reinforced-membrane structure. The difference in this instance is the extreme flexibility the rays have. Unlike normal bone or cartilage rays are very flexible with a modulus of about 1GPa. The supporting rays are depicted as nonlinear Euler–Bernoulli beams with three-dimensional deformability. Despite the fact that the real fin rays are non-uniform, anisotropic and have curvatures actively controlled by offsets of tendons linked to their bases, for simplicity we modeled the rays as uniform beams with circular cross-sections and passive deformations only. By this definition, these rays were able to sustain stretching, bending and twisting loads. Based upon the Euler-Lagrangian dual-coordinate approach and the robust Euler parameters, this method achieved fully-nonlinear simulation of arbitrary ray deformations. A finite difference algorithm, the modified box method, was then employed to solve these nonlinear equations.

To model the collagen membrane that forms the fabric of the fin we idealized the rest of the fin as a thin-foil that could sustain stretching/compression but not bending. This was done by using a distribution of spring-dampers between neighboring rays. This structural model was then incorporated into a boundary-element hydrodynamic model to achieve coupled fluid–structure interaction simulation. The hydrodynamic forces resulting from the surrounding fluid reacted directly on this membrane model in each of the proceding models.

9-Ray Caudal Fin Model:

The first model developed to study the effects of flexible fin rays was a 9-ray fin. This fin model was built to resemble the caudal fin (tail fin) of fish. As seen below the trapezoidal shape of our model (C) was designed to emulate the caudal tail on the left (A). The rays are represented as lines in the fin diagram below.

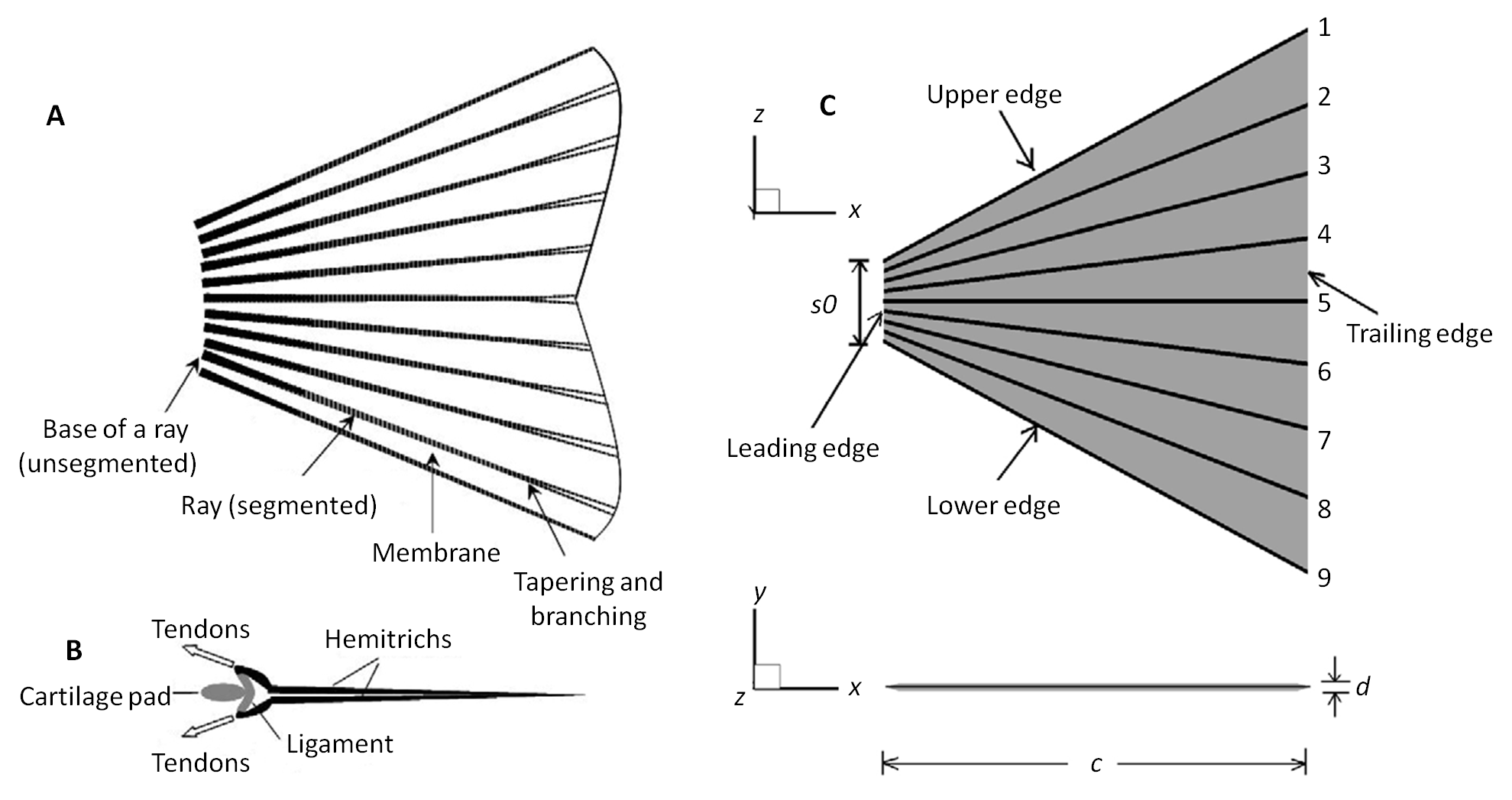(A) Schematic showing a typical ray-strengthened caudal fin [modified from Alben et al. (Alben et al., 2007)]. We note that the rays are segmented and are tapered and branched near the trailing edge. (B) The dorsal view of the internal structure of a ray [courtesy of S. Alben and the Royal Society (Alben et al., 2007)]. (C) A geometrically and structurally simplified fin employed in the present modeling study.

The caudal tail on a fish moves in a swaying motion. Therefore, in this analysis we considered a three-dimensional flapping motion of the fin in combination with a constant forward speed. A flapping motion was actuated by imposing sway-yaw motions on each ray. Two motions were defined: a homocercal mode, and a heterocercal mode. The homocercal mode had dorsal ventral symmetry (up and down), while the heterocercal mode had dorsal ventral asymmetry.

15-Ray Pectoral Fin Model:

Building off of the 9-ray caudal fin tests a 15-ray pectoral fin model was developed. In contrast to the previous model this model was developed in order to study flexible rays in lift-based propulsion. The fins shape resembles a simplified pectoral fin with a straight baseline and a curved tip, as shown in the diagram below. The model fin has 15 rays modeled as described above with tapered ends.

Geometry and internal structure of the fin. x0, length of baseline; d,thickness of fin.

In this study the fin underwent a translational motion in the x direction with constant speed U. To achieve lift-based thrust generation, a dorso–ventral flapping motion was activated by rotating each individual ray around the baseline. The forces and propulsive efficiency was then calculated using the numerical methods mentioned above.

12-Ray Pectoral Fin Model:

In the twelve-ray configuration a simple trapezoidal shape was used as seen below. The length of Ray 1 was L and the length of Ray 12 was 0.3L. The length of the rays was chosen so that the tip and baseline both formed lines for simplicity. Other than the shape the general structure was modeled the same in this modified fin as the previous with the membrane modeled as simple springs and the rays modeled as Euler-Bernoulli non-linear beams.

Schematic showing the 12-ray pectoral fin model. Rays numbered 1 through 12 with x-z orientation specified.

Although the structure was similar to the previous caudal model the new model held several new advances: (1) we considered much more complicated and realistic fin kinematics including anteroposterior, dorsoventral and baseline pitching motions enabled by synchronized ray rotations and reorientation of the baseline; (2) we considered a more realistic fin flexibility in which the rays had different stiffness; and (3) the hydrodynamic effects of both the phase lag between rays and the baseline pitching motion were explored. This model included two different designs. The first follows the same style as the previous models in that all of the rays had the same properties; whereas in the second design the leading edge ray had twice the diameter as the others equating to fifteen times the stiffness. The two designs, labeled Fin A and Fin B respectively, were tested with the same numerical methods and their results compared.

Tests & Results:

Performance of the 9-Ray Caudal Fin Model:

Kinematically, we incorporate both a homocercal mode with dorso-ventral symmetry and a heterocercal mode with dorso-ventral asymmetry. Using the homocercal mode, our results demonstrate that the anisotropic deformability of the ray reinforced fin significantly increases its capacity for force generation. This performance enhancement manifests as increased propulsion efficiency, reduced transverse force and reduced sensitivity to kinematic parameters. Further reduction in transverse force was observed when testing the heterocercal mode. In the heterocercal model, the fin also generated a small lifting force, which may be important in vertical maneuvers. Via three-dimensional flow visualization, a chain of vortex rings is observed in the wake. Detailed features of the wake, e.g. the orientation of the vortex rings in the heterocercal mode, agreed with predictions based upon particle image velocimetry (PIV) measurements of flow around live fish. A simulation of the resulting flow field from the homocercal and heterocercal modes of fin motion can be seen below.

Resulting flow field from heterocercal mode fin motion	Resulting flow field from homocercal mode fin motion

Performance of the 15-Ray Pectoral Fin Model:

Our results indicate that the hydrodynamic performance of such a system is determined by its frequency of motion (represented by the Strouhal number), phase difference among the rays, as well as structural properties of the rays. By varying the phases of the rays, the fin achieves a combination of roll and pitch motions. Based on this mechanism the effective angle of attack at the leading edge as well as the shape of the fin can be adjusted so that the thrust generation and propulsion efficiency can be optimized. With properly chosen kinematic parameters, positive thrust is observed in most of the down stroke-upstroke period. High propulsion efficiency (with a peak value of ~0.8 within the range of parameters considered in this study) is observed. Further investigation shows that performance of the system depends not only upon the maximum phase lag between all the rays, but also upon the detailed distribution of the phases.

In studying the effect of passive deformation of the fin due to structural flexibility of the rays we found that such passive deformations indeed increase the thrust generation as well as the propulsion efficiency [although the increase in efficiency is not as significant as in the case of caudal fins]. By visualizing the near-body flow field we find that a primary effect of structural flexibility is the reduction of the effective angle of attack, which suggests a mechanism for the change in performance.

Performance of the 12-Ray Pectoral Fin Model:

This more complete 12-ray model had novel results. It was proven that flexible rays alone do not increase the efficiency of propulsion. All the rays of Fin A had identical stiffness and strength properties. But as you can see in the graphs below Fin A displayed worse propulsion characteristics then did the control rigid ray model. Initially it would seem that flexible fins may actually be a disadvantage to labriform fish. However, simply strengthening the leading edge fin ray drastically changed the characteristics. Represented by Fin B, the reinforced leading edge fins displayed better propulsive characteristics than both Fin A and the control rigid fins. From these tests we concluded that strengthening of the ray at the leading edge plays a pivotal role in performance enhancement by reducing the effective angle of attack and decreasing the power expenditure during the recovery stroke.

Variations of (A) thrust coefficient (CT), (B) lateral force coefficient (Cy), (C) lift coefficient (CL) and (D) energy expenditure over one period for the fin with rigid rays (dotted lines), fin A (dashed lines) and fin B (solid lines). St=0.4, Ψ12=60 de

Vortex shedding of Undulating Fish:

Using boundary element method various tests were run on simulated bodies making undulating motions. These tests were meant to determine the style of the vortex shed while fish moved through the water and how these would affect the fish’s motion. During one full cycle of fish undulation a coupled pair of vortex rings is created in the wake of the moving fish. These pairs spin in opposite directions from each other. This effect is shown in the animation below.

Flow Around Rays of Varying Stiffness:

Using the immersed boundary method coupled with the Euler-Bernoulli non-linear beam method results tests were run, analyzing the change in flow patterns resulting from different flexibilities of fish fin rays. The results of the varying tests can be seen below.